Microsoft Word - Non-Standard Multiplication Methods for Parents Letter.docx

Compiled by Alycia Zimmerman for Classroom Use.

A Guide for Parents to Non-Standard Methods for Multi-Digit Multiplication

(Compiled by Alycia Zimmerman, 2015)

The area method, also sometimes called the box method, is an alternative to the standard algorithmic method

for long (multi-digit) multiplication. Both of these methods use the distributive property for multiplication but

they differ in how the partial products are calculated and written. The “grid method” is similar to the area

method, but it’s not proportional. That is, the grid boxes aren’t drawn to represent the sizes of the parts being

multiplied.

The standard algorithm (vertical algorthim) is generally a faster method but, unlike the area or grid methods,

it does not promote understanding or encourage the development of mathematical thinking. Students rarely

understand why they are carrying numbers or what that “placeholder zero” is all about in the second row of

calculations. It is best to introduce children to long multiplication with the area method/grid method before

using the standard algorithm. The area method also supports the important ability to estimate answers.

While these methods may seem new to many people, the grid method has been the preferred method taught in

elementary schools in the UK and Australia for more than twenty years, with excellent research-backed results.

It is also the first method taught with the Singapore Math curriculum, and it has been used in progressive

schools in the U.S. for at least the past 15 years. So, these strategies are not really new pedagogy at all, and

there is a lot of research that supports introducing long-multiplication this way.

This is not to impose a value judgment upon students for using one method over another. We value many things

in student mathematicians – efficiency, accuracy, flexibility, reliability, and understanding. Depending on a

student’s individual development and circumstances, some methods may be better suited for that student at

times than others. For students who already learned the traditional “vertical algorithm,” we do not want them to

abandon this method or see it as less worthy. However, by learning these other methods, they will have a

reliable system to check their work by using two methods. (Also, note that the students will be required to

demonstrate an understanding of the area/grid methods of multiplication on the fourth grade state math exam.)

So what does this all look like in action? Read on for examples and explanations …

AREA METHOD for Multiplication:

The area method relates the students’ understanding of area as a two-dimensional representation of

multiplication (length x width) to “Partial Products Multiplication” – that is, when each place-value part of a

number is multiplied by the other parts. This builds upon their basic understanding of arrays (developed in

second grade.)

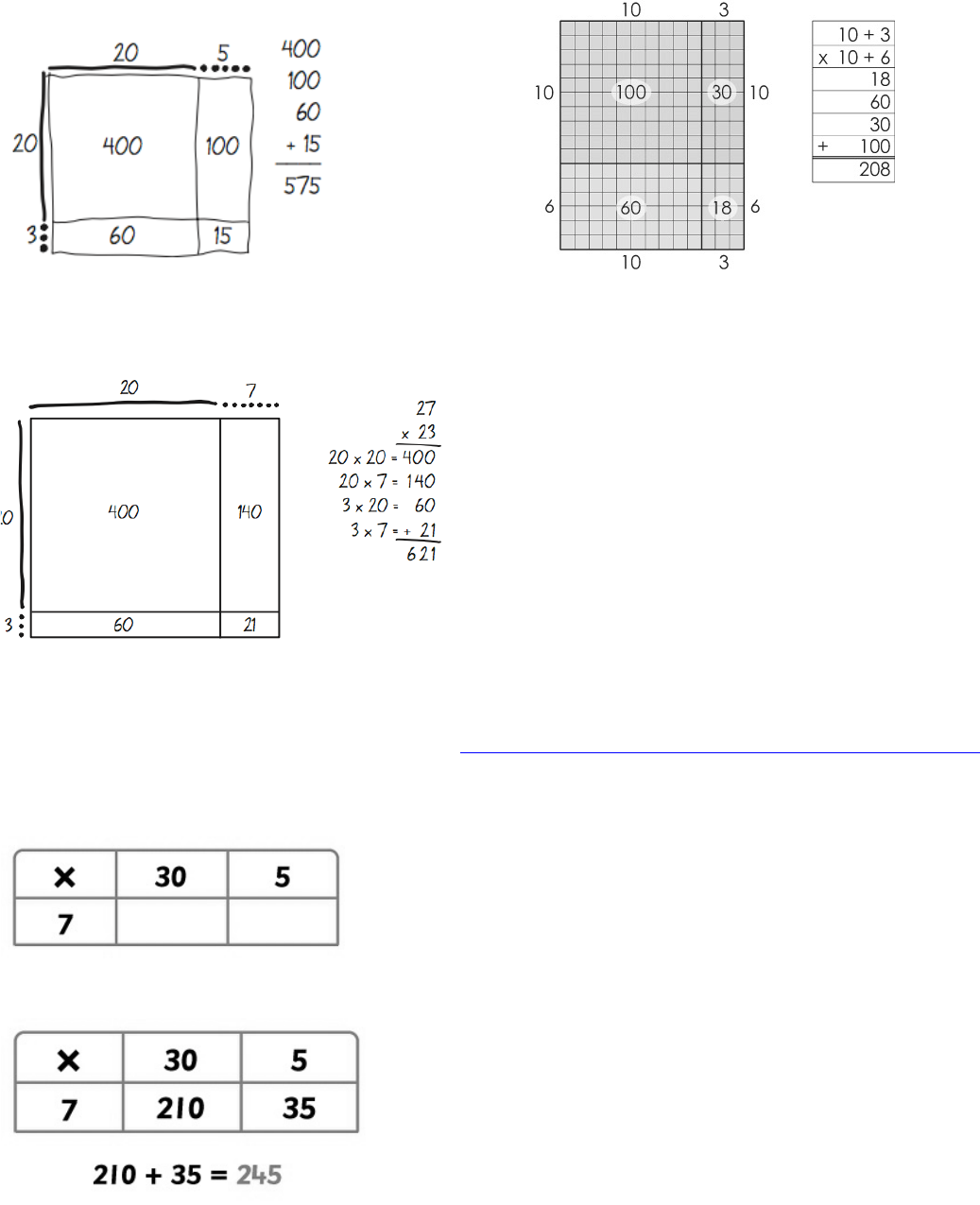
This area diagram (below) for 18 x 12 builds on the students’ understanding of area, and allows students to

visualize all of the discreet parts that are multiplied (partial products) and then added to get the total product:

Compiled by Alycia Zimmerman for Classroom Use.

Diagram A: The small markings outside of the grid represent the expanded-form parts – the tens and the ones

parts. It is a visual cue for students to remember how this model relates to area. Diagram B: If students were to

create an area model to scale on graph paper, the proportional parts would be immediately evident.

(Diagram A) (Diagram B)

This model demonstrates how the area model (in this case for 27 x 23) relates to the four “partial products”

problems from the distributive property.

GRID METHOD for Multiplication:

For more background on Grid Multiplication, see: http://en.wikipedia.org/wiki/Grid_method_multiplication.

Examples:

To calculate 35 × 7, set it out in a grid like this: (This arrangement is based on the expanded form of the #’s)

Multiply each pair of numbers and write them in the grid. Then add the two products (e.g. answers to the

multiplications) to find the answer.

Compiled by Alycia Zimmerman for Classroom Use.

The grid method can also be used for more difficult multiplication, such as 35 x 26.

Here’s an example of what Grid Multiplication will look like for a 3-digit times 2-digit scenario.

(Note: The addition step has been compressed and done mentally in this example. We encourage the students to

always write out their addition of the partial products to prevent careless errors.)

Partial Products Method for Multiplication:

The Partial Products Method uses the same sets of calculations as the grid method and area method, but without

the organizational structure of the grid. I find that students tend to be more reliable in their calculations when

they use the grid for support – the grid makes sure that they accurately multiply all of the correct parts.

However, this is also an approved method, and one that some teachers emphasize on its own. (I demonstrate this

method, as it relates to the Grid Method, but don’t put a lot of emphasis on this approach.)

The entire Partial Products Algorithm is built on the premise of children thinking of numbers in pieces. We

begin with children looking at problems horizontally so that they are more concerned with decomposing the

number into its pieces than a procedure for solving the problem.

Compiled by Alycia Zimmerman for Classroom Use.

How Do These Models (Area Method and Grid Method) Relate to Good Old-Fashioned Multiplication?

You’ll see in the examples below that the grid method relates to the 4-Part Model (AKA: Partial Products

Method) – and the 4-Part Model relates to the standard algorithm in turn. {The partial products 210 + 42 = the

252 from the first line of the standard algorithm products; the partial products 2100 + 420 are the same as the

second line of the standard algorithm (2,520).}