Calculus 2 Tutor
Worksheet 7
Integration by Partial Fractions

Worksheet for Calculus 2 Tutor, Section 7:
Integration by Partial Fractions
1. Write the following sums of fractions as ratios of two polynomials
P (x)
Q(x)
. In other
words, combine the fractions with a common denominator to produce one fraction.
(a)
1
x
+
2
x
(b)
1
x
+
1
x+1
(c)
1
x
2
+
1
x
(d)
1
x
2
+1
−
2
x
2
+2
c
2018 MathTutorDVD.com 1

(e)
x
x
2
+3x+2
−
2
x+10
(f)
x
3
x+2
−
x
3
2x
2
+1
(g)
1
x
3
−1
−
1
x
2
−1
+
1
x−1
. Hint: consider what the least common denominator is? Is there
a common factor between the denominators?
2. Decompose the following functions into partial fractions (that is; write it as the sum of
partial fractions):
(a)
1
x(x+1)
c
2018 MathTutorDVD.com 2

(b)
1
(x+2)(x−1)
(c)
x
(x−5)(x−6)
(d)
x+1
(x+5)(x+6)
(e)
1
(x−r
1
)(x−r
2
)
for r
1
, r
2
any real numbers and r
1
6= r
2
(f)
ax+b
(x−r
1
)(x−r
2
)
for a, b, r
1
, r
2
any real numbers and r
1
6= r
2
c
2018 MathTutorDVD.com 3

(g)
1
(x+1)(x+2)(x+3)
(h)
x+2
(x−3)(x−5)(x−7)
(i)
3x
2
+1
(
x−
1
2
)(
x−
1
3
)(
x−
1
4
)
3. Decompose the following functions into partial fractions:
(a)
x−1
x
2
c
2018 MathTutorDVD.com 4

(b)
2x+5
(x−1)
2
(c)
1
(x−1)(x−2)
2
(d)
ax+b
(x−r
1
)(x−r
2
)
2
(e)
x
x
2
+4x+5
c
2018 MathTutorDVD.com 5

(f)
x
3
(x
2
+2x+4)
2
(g)
x
2
x
3
−3x
2
+3x−1
(h)
x
4
(x−1)(x−2)(x−3)
(i) Challenge.
x
5
−4x
4
(x−1)
2
(x
2
+1)
4. Solve the following indefinite integrals using the partial fractions decomposition tech-
nique:
(a)
R
1
x(x+1)
dx
c
2018 MathTutorDVD.com 6

(b)
R
x−2
(
x+
1
3
)(
x+
1
4
)
dx
(c)
R
−
x
2
(x+1)(x−2)(x−3)
dx
(d)
R
x
2
+5
(x+1)
3
dx
(e)
R
1
x(x
2
+1)
dx
c
2018 MathTutorDVD.com 7

5. Challenge. Solve the following indefinite integrals using the partial fractions decom-
position technique:
(a)
R
x
4
(x−1)(x
2
+2)
dx
(b)
R
4
x(x
2
+2x+4)
dx
(c)
R
1
sin
2
x+sin x cos x
dx
c
2018 MathTutorDVD.com 8

Answer key.
1. Combining sums of fractions.
1(a). Answer:
3
x
. Since the fractions
1
x
and
2
x
share a common denominator, we can
combine the numerators:
1
x
+
2
x
=
1 + 2
x
=
3
x
which is our answer:
3
x
.
c
2018 MathTutorDVD.com 9

1(b). Answer:
2x + 1
x
2
+ x
. The fractions
1
x
and
1
x+1
do not share a common denominator
as they are written, but we can combine them by writing them in terms of a least
common denominator. The least common denominator is the product of the two
denominators:
x(x + 1)
So we need to write both fractions in terms of this least common denominator.
We write
1
x
=
1
x
·
x + 1
x + 1
=
x + 1
x(x + 1)
That is, we are taking the fraction
1
x
and multiply it by
x + 1
x + 1
= 1
to get the same fraction in terms of the least common denominator, x(x + 1).
Likewise, we write
1
x + 1
=
1
x + 1
·
x
x
=
x
x(x + 1)
That is, we multiply the second fraction
1
x+1
by the factor
x
x
= 1
to get the same fraction in terms of the least common denominator, x(x + 1).
Then, we can combine the fractions:
x + 1
x(x + 1)
+
x
x(x + 1)
=
(x + 1) + (x)
x(x + 1)
=
2x + 1
x(x + 1)
Lastly, we can simplify the denominator by writing
x(x + 1) = x
2
+ x
to write it as
2x + 1
x
2
+ x
which is our final answer.
c
2018 MathTutorDVD.com 10

1(c). Answer:
x + 1
x
2
. The fractions
1
x
and
1
x
2
do not have a common denominator.
However, they can be written as fractions in terms of a common denominator x
2
.
The fraction
1
x
2
is already written as a fraction in x
2
. The fraction
1
x
can be written
as
1
x
=
x
x
2
Then, we can write
x
x
2
+
1
x
2
=
x + 1
x
2
which is our answer:
x + 1
x
2
.
c
2018 MathTutorDVD.com 11
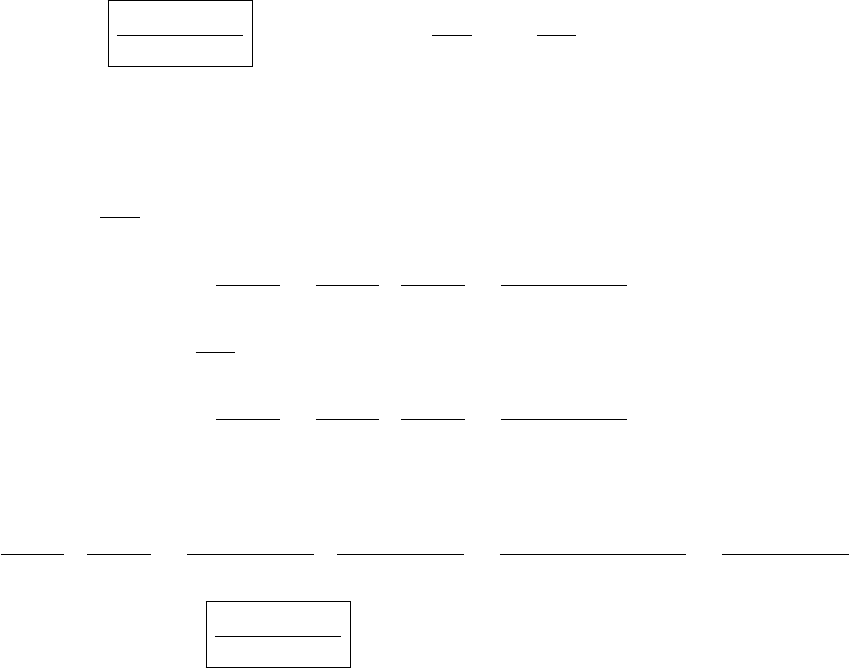
1(d). Answer:
−x
2
x
4
+ 3x
2
+ 2
. The fractions
1
x
2
+1
and
2
x
2
+2
do not have a common
denominator. The least common denominator is the product of the denominators:
x
2
+ 1
x
2
+ 2
= x
2
x
2
+ 2
+ 1
x
2
+ 2
= x
4
+ 2x
2
+ x
2
+ 2 = x
4
+ 3x
2
+ 2
We write
1
x
2
+1
in terms of this common denominator:
1
x
2
+ 1
=
1
x
2
+ 1
·
x
2
+ 2
x
2
+ 2
=
x
2
+ 2
x
4
+ 3x
2
+ 2
We can also write
2
x
2
+2
in terms of this common denominator as
2
x
2
+ 2
=
2
x
2
+ 2
·
x
2
+ 1
x
2
+ 1
=
2x
2
+ 2
x
2
+ 3x
2
+ 2
Then, we can subtract:
1
x
2
+ 1
−
2
x
2
+ 2
=
x
2
+ 2
x
4
+ 3x
2
+ 2
−
2x
2
+ 2
x
4
+ 3x
2
+ 2
=
x
2
+ 2 − (2x
2
+ 2)
x
4
+ 3x
2
+ 2
=
−x
2
x
4
+ 3x
2
+ 2
This is the answer:
−x
2
x
4
+ 3x
2
+ 2
.
c
2018 MathTutorDVD.com 12

1(e). Answer:
−x
2
+ 4x − 4
x
3
+ 13x
2
+ 32x + 20
. Since these fractions do not have a common
denominator, we can combine them with a common denominator that is the prod-
uct of the denominators:
x
2
+ 3x + 2
(x + 10) = x
x
2
+ 3x + 2
+ 10
x
2
+ 3x + 2
= x
3
+ 3x
2
+ 2x + 10x
2
+ 30x + 20 = x
3
+ 13x
2
+ 32x + 20
Then, we can write both fractions in terms of this common denominator:
x
x
2
+ 3x + 2
=
x
x
2
+ 3x + 2
·
x + 10
x + 10
=
x
2
+ 10x
x
3
+ 13x
2
+ 32x + 20
and
2
x + 10
=
2
x + 10
·
x
2
+ 3x + 2
x
2
+ 3x + 2
=
2x
2
+ 6x + 4
x
3
+ 13x
2
+ 32x + 20
Then, we can compute the difference:
x
x
2
+ 3x + 2
−
2
x + 10
=
x
2
+ 10x
x
3
+ 13x + 32x + 20
−
2x
2
+ 6x + 4
x
3
+ 13x
2
+ 32x + 20
=
(x
2
+ 10x) − (2x
2
+ 6x + 4)
x
3
+ 13x
2
+ 32x + 20
which is
−x
2
+ 4x − 4
x
3
+ 13x
2
+ 32x + 20
.
c
2018 MathTutorDVD.com 13

1(f).
x
3
x+2
−
x
3
2x
2
+1
. Answer:
2x
5
− x
4
− x
3
2x
3
+ 4x
2
+ x + 2
. The fact that the numerators are the
same is not relevant in this problem because the denominators are different. Also,
the fact that the degree of the numerators is greater than the degree of the de-
nominators does not affect how we combine the fractions. We still need to find
the common denominator
(x + 2)
2x
2
+ 1
= 2x
3
+ 4x
2
+ x + 2
Then we write
x
3
x + 2
=
x
3
x + 2
·
2x
2
+ 1
2x
2
+ 1
=
2x
5
+ x
3
2x
3
+ 4x
2
+ x + 2
and
x
3
2x
2
+ 1
=
x
3
2x
2
+ 1
·
x + 2
x + 2
=
x
4
+ 2x
3
2x
3
+ 4x
2
+ x + 2
Then we can take the difference:
x
3
x + 2
−
x
3
2x
2
+ 1
=
2x
5
+ x
3
2x
3
+ 4x
2
+ x + 2
−
x
4
+ 2x
3
2x
3
+ 4x
2
+ x + 2
and then we subtract the numerators to get
2x
5
+ x
3
−
x
4
+ 2x
3
= 2x
5
− x
4
− x
3
so the answer is
2x
5
− x
4
− x
3
2x
3
+ 4x
2
+ x + 2
.
c
2018 MathTutorDVD.com 14

1(g). Answer:
x
3
+ x
2
+ 2x + 1
x
4
+ x
3
− x − 1
. The least common denominator is not actually the
product of all the denominators. They all have the common factor x −1! (We can
verify that they are all multiples of x − 1 by checking that they all have a root at
x = 1; that is, that they are all zero at x = 1.) The first denominator x
3
− 1 is
x
3
− 1 = (x − 1)
x
2
+ x + 1
and the second denominator x
2
− 1 is
x
2
− 1 = (x − 1) (x + 1)
Then, the common denominator is
(x − 1) (x + 1)
x
2
+ x + 1
=
x
2
− 1
x
2
+ x + 1
= x
4
+ x
3
− x − 1
We can put all of the fractions in terms of the common denominator as follows.
The first fraction is
1
x
3
− 1
·
x + 1
x + 1
=
x + 1
x
4
+ x
3
− x − 1
The second fraction is
1
x
2
− 1
·
x
2
+ x + 1
x
2
+ x + 1
=
x
2
+ x + 1
x
4
+ x
3
− x − 1
The third fraction is
1
x − 1
·
(x + 1)(x
2
+ x + 1)
(x + 1)(x
2
+ x + 1)
=
1
x − 1
·
x
3
+ 2x
2
+ 2x + 1
x
3
+ 2x
2
+ 2x + 1
=
x
3
+ 2x
2
+ 2x + 1
x
4
+ x
3
− x − 1
Then the fractions combine to yield
(x + 1) − (x
2
+ x + 1) + (x
3
+ 2x
2
+ 2x + 1)
x
4
+ x
3
− x − 1
=
x
3
+ x
2
+ 2x + 1
x
4
+ x
3
− x − 1
which is our answer:
x
3
+ x
2
+ 2x + 1
x
4
+ x
3
− x − 1
.
c
2018 MathTutorDVD.com 15
2. Basic partial fractions decompositions:
2(a). Answer:
1
x
−
1
x + 1
. The partial fractions technique tells us that
1
x(x + 1)
=
A
x
+
B
x + 1
for some constants A, B. That is, the function
1
x(x+1)
can be written as some mul-
tiple of the partial fractions
1
x
and
1
x+1
. To find out the constants of multiplication
A, B, we multiply through the equation by x(x + 1). We have that
1
x(x + 1)
· x(x + 1) =
A
x
· x(x + 1) +
B
x + 1
· x(x + 1)
In each term, there is a cancellation. After making the cancellations, we have
that
1 = A(x + 1) + Bx
This must be true for all values of x. Particularly, it must be true for x = 0 where
we have
1 = A(0 + 1) + B(0)
which means
A = 1
It also must be true for x = −1 when we have
1 = A(−1 + 1) + B(−1)
which shows that
B = −1
We could also solve for A, B by rewriting the equation as
1 = (A + B)x + A
and then solving the system of equations
A + B = 0, A = 1
c
2018 MathTutorDVD.com 16

so that the coefficients of the x term is zero on both sides and the coefficient of
the constant term is one on both sides. Then, to get the answer, we simply plug
in A, B into the form
A
x
+
B
x+1
to get the answer:
1
x
−
1
x + 1
.
c
2018 MathTutorDVD.com 17

2(b). Answer:
1
3
x − 1
−
1
3
x + 2
. The partial fractions technique tells us that
1
(x+2)(x−1)
can be written as
A
x − 1
+
B
x + 2
for some constants A, B. Our technique is to solve the equation
1
(x + 2)(x − 1)
=
A
x − 1
+
B
x + 2
for A, B. To solve this, we multiply through by (x + 2)(x − 1) to get
1
(x + 2)(x − 1)
· (x + 2)(x − 1) =
A
x − 1
· (x + 2)(x − 1) +
B
x + 2
· (x + 2)(x − 1)
which simplifies to
1 = A(x + 2) + B(x − 1)
We can find the values of A, B in two ways. First we can set it up as a system of
equations:
1 = (A + B)x + (2A − B)
or
0x + 1 = (A + B)x + (2A − B)
For these sides to be the same thing, the coefficients of x and the constant need
to be the same; that is,
A + B = 0
1 = 2A − B
The first equation tells us that −B = A so the second equation becomes
3A = 1, A =
1
3
which means
B = −
1
3
c
2018 MathTutorDVD.com 18

We could also solve for A, B by plugging in values to make each term cancel. If
we plug in x = −2 we have
1 = A(−2 + 2) + B(−2 − 1)
which means
1 = −3B, B = −
1
3
and if we plug in x = 1 we have
1 = A(1 + 2) + B(1 − 1)
which means
1 = 3A, A =
1
3
These are the same answers we got in the first method! Therefore the answer
of the form
A
x−1
+
B
x+2
is
1
3
x − 1
−
1
3
x + 2
where the minus sign is because B is a
negative quantity.
c
2018 MathTutorDVD.com 19

2(c). Answer:
6
x − 6
−
5
x − 5
. According to the partial fractions technique, this can
be written as
A
x − 5
+
B
x − 6
for some A, B. To find the A, B for which this is true, we solve:
x
(x − 5)(x − 6)
=
A
x − 5
+
B
x − 6
Then we multiply through by (x − 5)(x − 6) to find
x = A(x − 6) + B(x − 5)
We can solve this in two ways: we can write
1x + 0 = (A + B)x + (−6A − 5B)
For these sides to be equal, the coefficient of x and the coefficient of the constant
must be the same. That is,
A + B = 1
−6A − 5B = 0
Since by the first equation B = 1 − A, we can plug this into the second equation
to get
−6A − 5(1 − A) = −A − 5 = 0
so
A = −5
which means
B = 6
We could get these same results by plugging in select values of x into the equa-
tion
x = A(x − 6) + B(x − 5)
c
2018 MathTutorDVD.com 20

At x = 6, we have that
6 = A(6 − 6) + B(6 − 5)
which means that
B = 6
Likewise, at x = 5, we have that
5 = A(5 − 6) + B(5 − 5)
which means
A = −5
Therefore, our answer of the form
A
x−5
+
B
x−6
is
6
x − 6
−
5
x − 5
where the negative
sign is because A = −5.
c
2018 MathTutorDVD.com 21

2(d). Answer:
5
x + 6
−
4
x + 5
. According to the partial fractions technique, we write
x + 1
(x + 5)(x + 6)
=
A
x + 5
+
B
x + 6
for some A, B. Multiplying by (x + 5)(x + 6) yields
x + 1 = A(x + 6) + B(x + 5)
We can solve for A, B in two different ways. First we could write
x + 1 = (A + B)x + (6A + 5B)
which means that
A + B = 1, 6A + 5B = 1
Writing B = 1 − A based on the first equation, we can write
6A + 5(1 − A) = 1
which means that
A = −4
and therefore
B = 5
We could get the same results by plugging in strategic values of x into x + 1 =
A(x + 6) + B(x + 5). This must be true at x = −6 when the first term will cancel;
there,
−5 = 0A + −B
which means
B = 5
Likewise it must be true at x = −5 where the second term will cancel; there,
−4 = A + 0B
c
2018 MathTutorDVD.com 22

which means
A = −4
Therefore the answer of the form
A
x+5
+
B
x+6
is
5
x + 6
−
4
x + 5
.
c
2018 MathTutorDVD.com 23

2(e). Answer:
1
r
1
−r
2
x − r
1
+
1
r
2
−r
1
x − r
2
. According to the partial fractions technique, we can
write
1
(x − r
1
)(x − r
2
)
=
A
x − r
1
+
B
x − r
2
for some A, B and any x. Multiplying through as previously, we get that
1 = A(x − r
2
) + B(x − r
1
)
This must be true for all x; it is true at x = r
2
where
1 = 0A + B(r
2
− r
1
)
or
B =
1
r
2
− r
1
It also is true at x = r
1
where
1 = A(r
1
− r
2
) + 0B
or
A =
1
r
1
− r
2
Then the answer is
1
r
1
−r
2
x − r
1
+
1
r
2
−r
1
x − r
2
. We see why it is important that r
1
6= r
2
- if
this were the case, there would be no answer of this form since it would be
1
(x−r
1
)
2
which does not simplify.
c
2018 MathTutorDVD.com 24

2(f). Answer:
ar
1
+b
r
1
−r
2
x − r
1
+
ar
2
+b
r
2
−r
1
x − r
2
. According to the partial fractions technique, we can
write
ax + b
(x − r
1
)(x − r
2
)
=
P
x − r
1
+
Q
x − r
2
where we pick the constants P, Q to avoid confusion with the constants a, b. To
solve for P, Q we need to multiply through by (x − r
1
)(x − r
2
) to get
ax + b = P (x − r
2
) + Q(x − r
1
)
This is true for all x; it is true for x = r
2
when the first term will cancel. There,
ar
2
+ b = P (0) + Q(r
2
− r
1
)
which means
Q =
ar
2
+ b
r
2
− r
1
It is also true for x = r
1
where
ar
1
+ b = P (r
1
− r
2
) + Q(0)
which means that
P =
ar
1
+ b
r
1
− r
2
This allows us to determine the answer of the form
P
x−r
1
+
Q
x−r
2
; it is
ar
1
+b
r
1
−r
2
x − r
1
+
ar
2
+b
r
2
−r
1
x − r
2
.
c
2018 MathTutorDVD.com 25

2(g). Answer:
1
2
x + 1
−
1
x + 2
+
1
2
x + 3
. The presence of three terms in the denomina-
tor does not change the approach. According to partial fractions, we can write
1
(x + 1)(x + 2)(x + 3)
=
A
x + 1
+
B
x + 2
+
C
x + 3
for any x and some A, B, C. To solve for A, B, C we need to multiply through by
(x + 1)(x + 2)(x + 3). After our cancellations, we have that
1 = A(x + 2)(x + 3) + B(x + 1)(x + 3) + C(x + 1)(x + 2)
This is true for all values of x. At the value x = −1, all the x + 1 terms cancel
which means that the last two terms are zero! So we have
1 = A(−1 + 2)(−1 + 3) + 0B + 0C
which means that
A =
1
2
At the value x = −2, all the x + 2 terms which means that the first and third terms
zero out. So we have
1 = 0A + B(−2 + 1)(−2 + 3)
which means that
B = −1
At the value x = −3 all the x + 3 terms cancel which means that the first and
second terms zero out. So we have
1 = 0A + 0B + C(−3 + 1)(−3 + 2)
which means that
C =
1
2
So the answer of the form
A
x+1
+
B
x+2
+
C
x+3
is
1
2
x + 1
−
1
x + 2
+
1
2
x + 3
.
c
2018 MathTutorDVD.com 26

2(h). Answer:
5
8
x − 3
−
7
4
x − 5
+
9
8
x − 7
. According to the partial fractions method, we
write
x + 2
(x − 3)(x − 5)(x − 7)
=
A
x − 3
+
B
x − 5
+
C
x − 7
To solve for A, B, C we can multiply through by (x − 3)(x − 5)(x − 7) to get
x + 2 = A(x − 5)(x − 7) + B(x − 3)(x − 7) + C(x − 3)(x − 5)
This is true at all values of x. At x = 3 the last two terms will cancel; there we
have
5 = A(3 − 5)(3 − 7) + 0B + 0C
which means that
A =
5
8
At x = 5 the first and third terms cancel; there we have
7 = 0A + B(5 − 3)(5 − 7) + 0C
which means that
B = −
7
4
At x = 7 the first two terms cancel; there we have
9 = 0A + 0B + C(7 − 3)(7 − 5)
which means
C =
9
8
Therefore, our answer of the form
A
x−3
+
B
x−5
+
C
x−7
is
5
8
x − 3
−
7
4
x − 5
+
9
8
x − 7
.
c
2018 MathTutorDVD.com 27

2(i). Answer:
42
x −
1
2
−
96
x −
1
3
+
57
x −
1
4
. According to the partial fractions method, we
can write
3x
2
+ 1
x −
1
2
x −
1
3
x −
1
4
=
A
x −
1
2
+
B
x −
1
3
+
C
x −
1
4
We need to determine the constants A, B, C. This we can do by multiplying
through by
x −
1
2
x −
1
3
x −
1
4
to get
3x
2
+ 1 = A
x −
1
3
x −
1
4
+ B
x −
1
2
x −
1
4
+ C
x −
1
2
x −
1
3
This is true at x =
1
2
; there,
3
4
+ 1 = A
1
2
−
1
3
1
2
−
1
4
+ 0B + 0C
which means
7
4
= A
1
6
·
1
4
or
A = 42
Likewise we can determine B by plugging in x =
1
3
; there,
3
9
+ 1 = 0A + B
1
3
−
1
2
1
3
−
1
4
+ 0C
or
4
3
= B
−
1
6
·
1
12
which simplifies to
B = −96
Finally, at x =
1
4
we have
3
16
+ 1 = 0A + 0B + C
1
4
−
1
2
1
4
−
1
3
or
19
16
= C
1
4
·
1
12
c
2018 MathTutorDVD.com 28

which means
C = 57
Therefore the answer in the desired form
A
x −
1
2
+
B
x −
1
3
+
C
x −
1
4
is
42
x −
1
2
−
96
x −
1
3
+
57
x −
1
4
.
c
2018 MathTutorDVD.com 29

3. Decompose the following functions into partial fractions:
3(a). Answer:
1
x
−
1
x
2
. The partial fractions decomposition technique tells us that
this function can be written as
x − 1
x
2
=
A
x
+
B
x
2
for some constants A, B. We need to find these constants A, B. Multiplying
through by x
2
, we see that
x − 1 = Ax + B
For this to be true for all x, we need
A = 1, B = −1
Then the answer is
1
x
−
1
x
2
. Of course, we could get to the same answer by
simply splitting up the function:
x − 1
x
2
=
x
x
2
−
1
x
2
which simplifies to the same answer
1
x
−
1
x
2
However, in general there is no simple way to get to this answer, so we need to
use partial fractions techniques for the general case of a square in the denomi-
nator.
c
2018 MathTutorDVD.com 30

3(b). Answer:
2
(x − 1)
+
7
(x − 1)
2
. The partial fractions decomposition technique tells
us that this function can be written as
2x + 5
(x − 1)
2
=
A
x − 1
+
B
(x − 1)
2
for some constants A, B. We need to find these constants. Multiplying through
by (x − 1)
2
, we see that
2x + 5 = A(x − 1) + B
This is true for all values of x. In particular, it is true for x = 1 where we have
2(1) + 5 = A(0) + B
or
B = 7
Also, for this to be true, the coefficients of x have to be equal, which means
A = 2
Therefore the answer of the form
A
x−1
+
B
(x−1)
2
is
2
(x − 1)
+
7
(x − 1)
2
. The new
element in this problem is that, if there is a square or higher exponent in the
denominator of the fraction we seek to decompose, there are terms with all of the
lesser exponents of that factor in the decomposition.
c
2018 MathTutorDVD.com 31

3(c). Answer:
1
x − 1
−
1
x − 2
+
1
(x − 2)
2
. Here, by the partial fractions decomposition
technique, we know that in the decomposition there will be three different terms:
1
(x − 1)(x − 2)
2
=
A
x − 1
+
B
x − 2
+
C
(x − 2)
2
for some A, B, C. Because of the (x − 2)
2
in the denominator, there is a x − 2
term in addition to the x − 2 term in the partial fractions expansion. To find the
coefficients A, B, C we need to multiply by (x − 1)(x − 2)
2
. We have that
1 = A(x − 2)
2
+ B(x − 1)(x − 2) + C(x − 1)
for all x. This is particularly true for x = 2, where the first terms zero: at x = 2 we
have
1 = A(0) + B(0) + C(2 − 1)
which means that
C = 1
It is also true for x = 1, where the last two terms zero; at x = 1 we have
1 = A(1 − 2)
2
+ B(0) + C(0)
which means that
A = 1
How do we find B? We need to expand the the expression with our new values
for A, C to see which value of B makes the sides match. However, this problem
spares us from needing to expand the whole expression. Instead, we can only
look at the x
2
term. The x
2
term is clearly
(A + B)x
2
on the right side; for this to match the x
2
term on the left side which is zero, we
need
A + B = 0
c
2018 MathTutorDVD.com 32

or
B = −1
Finally, we have all three terms A, B, C for our answer of the form
A
x − 1
+
B
x − 2
+
C
(x − 2)
2
The answer is
1
x − 1
−
1
x − 2
+
1
(x − 2)
2
.
c
2018 MathTutorDVD.com 33

3(d). Answer:
ar
1
+b
(r
1
−r
2
)
2
x − r
1
−
ar
1
+b
(r
1
−r
2
)
2
x − r
2
+
ar
2
+b
r
2
−r
1
(x − r
2
)
2
. This is a more general case of the pre-
vious problem. We solve it the same way:
ax + b
(x − r
1
)(x − r
2
)
2
=
P
x − r
1
+
Q
x − r
2
+
S
(x − r
2
)
2
where P, Q, S are the names of variables chosen to avoid confusion with a, b, r.
Multiplying by (x − r
1
)(x − r
2
)
2
we get
ax + b = P (x − r
2
)
2
+ Q(x − r
1
)(x − r
2
) + S(x − r
1
)
This is true for all x. We can find P, Q, S by first testing x = r
1
. There the terms
with Q and S zero out leaving us with
ar
1
+ b = P (r
1
− r
2
)
2
+ 0Q + 0S
which means that
P =
ar
1
+ b
(r
1
− r
2
)
2
At x = r
2
, the terms with P and Q cancel out leaving us with
ar
2
+ b = 0P + 0Q + S(r
2
− r
1
)
which means that
S =
ar
2
+ b
r
2
− r
1
How do we find the coefficient of Q? We could plug in x = 0 or some other
value but it would be really messy. Instead, we can examine the x
2
term of the
expression since it must be the same on both sides. On the the left the coefficient
of x
2
is zero. On the right the coefficient is P + Q. Then, we must have
P + Q = 0
or
Q = −
ar
1
+ b
(r
1
− r
2
)
2
Then we have all the coefficients P, Q, S for
P
x−r
1
+
Q
x−r
2
+
S
(x−r
2
)
2
, so we have our
answer:
ar
1
+b
(r
1
−r
2
)
2
x − r
1
−
ar
1
+b
(r
1
−r
2
)
2
x − r
2
+
ar
2
+b
r
2
−r
1
(x − r
2
)
2
.
c
2018 MathTutorDVD.com 34

3(e). Answer:
x
x
2
+ 4x + 5
. When we have a quadratic in the denominator, the first
step is to see if it is factorable. If it can be factored into (x − r
1
)(x − r
2
) there will
be a partial fractions expansion in the form
A
x − r
1
+
B
x − r
2
If the quadratic is factorable, it has a real root that is given by the quadratic equa-
tion. The quadratic formula
−b ±
√
b
2
− 4ac
2
applied to x
2
+ 4x + 5 yields
−4 ±
p
16 − 4(5)
2
=
−4 ±
√
−4
2
The discriminant b
2
− 4ac is negative which means that there are no real roots!
If there were roots r
1
and r
2
it could be factored as (x − r
1
)(x − r
2
). However,
because there are no real roots, there is no factorization. So the denominator
is irreducible. Since the decree of the numerator is less than the degree of the
numerator, the answer is already in the fully reduced form of a linear function
divided by an irreducible quadratic. So the answer is
x
x
2
+ 4x + 5
.
c
2018 MathTutorDVD.com 35

3(f). Answer:
x − 2
x
2
+ 2x + 4
+
8
(x
2
+ 2x + 4)
2
. This quadratic function is also irreducible
because its discriminant is negative:
b
2
− 4ac = 2
2
− 4(4) = −12
So it cannot be broken up into linear roots and is irreducible. Then, the partial
fractions technique for decomposition of a fraction with an irreducible quadratic
indicates that the answer is of the form
x
3
(x
2
+ 2x + 4)
2
=
A
1
x + B
1
x
2
+ 2x + 4
+
A
2
x + B
2
(x
2
+ 2x + 4)
2
To solve for A
1
, A
2
, B
1
, B
2
we need to multiply through by (x
2
+ 2x + 4)
2
. We have
that
x
3
= (A
1
x + B
1
)(x
2
+ 2x + 4) + (A
2
x + B
2
)
There are no values of x that we can plug in here to help us solve the problem
easily. Instead we need to match the coefficients of different powers of x for these
sides to be equal. We write
1x
3
+ 0x
2
+ 0x + 0 = A
1
x
3
+ 2A
1
x
2
+ 4A
1
x + B
1
x
2
+ 2B
1
x + 4B
1
+ A
2
x + B
2
Then we organize the right side by separating each power of x to write
1x
3
+ 0x
2
+ 0x + 0 = A
1
x
3
+ (2A
1
+ B
1
)x
2
+ (4A
1
+ 2B
1
+ A
2
)x + (4B
1
+ B
2
)
We match the coefficients of x
3
to find that
A
1
= 1
We match the coefficients of x
2
to tell us that
0 = 2A
1
+ B
1
Since A
1
= 1 this means that
B
1
= −2
c
2018 MathTutorDVD.com 36

Then we match the coefficients of x to tell us that
4A
1
+ 2B
1
+ A
2
= 0
Since A
1
= 1 and B
1
= −2 we have that
4 − 4 + A
2
= 0
or
A
2
= 0
Finally, to find the last coefficient, we know that
4B
1
+ B
2
= 0
Since B
1
= −2 we see that B
2
= 8. We have found all of the coefficients
A
1
, A
2
, B
1
, B
2
in the form
A
1
x+B
1
x
2
+2x+4
+
A
2
x+B
2
(x
2
+2x+4)
2
so we can write the answer:
x − 2
x
2
+ 2x + 4
+
8
(x
2
+ 2x + 4)
2
.
c
2018 MathTutorDVD.com 37

3(g). Answer:
1
x − 1
+
2
(x − 1)
2
+
1
(x − 1)
3
. To solve this problem, we need to fac-
torize the denominator to tell what sort of function it is. Are there irreducible
quadratics at play? Linear functions? The coefficients 1 and 3 that pair off indi-
cate that x = 1 might be a root and therefore x − 1 a factor. To determine the the
other factors, we need to divide:
x
3
− 3x
2
+ 3x − 1
x − 1
We could do this by performing polynomial long division. We could also solve for
the coefficients of the quadratic that will be the quotient of a cubic over a linear.
We solve
x
3
− 3x
2
+ 3x − 1
x − 1
= ax
2
+ bx + c
Multiplying through by x − 1, we get
x
3
−3x
2
+ 3x − 1 = ax
3
−ax
2
+ bx
2
−bx + cx − c = ax
3
+ (b − a)x
2
+ (c − b)x − c
where we group the terms by their power. All the coefficients must be equal, so
for the cubic term to be equivalent,
a = 1
For the quadratic term to be equal,
−3 = b − a = b − 1
so
b = −2
For the linear term to be equal,
3 = c − b = c − (−2) = c + 2
so
c = 1
c
2018 MathTutorDVD.com 38

Then, the quotient that contains the remaining factors is
x
2
− 2x + 1
The quadratic formula tells us that this has the twin roots x = 1 so it has the
square factor
x
2
− 2x + 1 = (x − 1)
2
The square factor (x − 1)
2
combines with the factor of x − 1 that we already
factored out, showing that (x − 1)
3
is the factorization of the function; that is,
x
3
− 3x
2
+ 3x − 1 = (x − 1)
3
Then, the partial fractions expansion will be in the form
x
2
(x − 1)
3
=
A
x − 1
+
B
(x − 1)
2
+
C
(x − 1)
3
according to the partial fractions decomposition technique - that is, according to
the technique, we can only expand with constants over powers of x −1. We only
need to solve for the constants A, B, C. We can do this by multiplying by (x −1)
3
to get
x
2
= A(x − 1)
2
+ B(x − 1) + C
which is true for all x. Plugging in x = 1 gives
1 = 0A + 0B + C
or
C = 1
We also can use the method that shows the equality of the coefficients of each
term. The B term and the C term don’t have powers of x
2
; only the A term. The
only x
2
term on the right side is Ax
2
which we know is equal to x
2
; therefore
A = 1
c
2018 MathTutorDVD.com 39

Finally, the constant term on the right side is
A − B + C
which we know to be equal to zero, the constant coefficient on the left side. Solv-
ing
A − B + C = 0
with the known values of A = C = 1 gives B = 2. Therefore the answer of the
form
A
x−1
+
B
(x−1)
2
+
C
(x−1)
3
is
1
x − 1
+
2
(x − 1)
2
+
1
(x − 1)
3
.
c
2018 MathTutorDVD.com 40

3(h). Answer: x + 6 +
1
2
x − 1
−
16
x − 2
+
81
2
x − 3
. We are not ready right away for the
partial fractions expansion, since the degree of the numerator (4) is higher than
that of the denominator (3). The partial fractions expansion can only be done on
the remainder that we can calculate in polynomial long division. In other words,
since the degree of the numerator is higher than the degree of the denominator,
we write
x
4
(x − 1)(x − 2)(x − 3)
= P (x) +
Q(x)
(x − 1)(x − 2)(x − 3)
where P is the whole polynomial result of long division and Q is the remainder
which much have a degree of 2 or less since the denominator has degree 3.
We also know that P is going to be a linear function since the degree of the
numerator is one higher than the degree of the denominator. As an alternative to
performing long division, we can simply solve for the coefficients of P and Q. We
write P = ax + b. Multiplying
x
4
(x − 1)(x − 2)(x − 3)
= ax + b +
Q(x)
(x − 1)(x − 2)(x − 3)
through by (x − 1)(x − 2)(x − 3) we get
x
4
= (ax + b)(x − 1)(x − 2)(x − 3) + Q(x)
or, expanding,
x
4
= (ax + b)(x
3
− 6x
2
+ 11x − 6) + Q(x)
which is
x
4
= ax
4
+ (−6a + b)x
3
+ (11a − 6b)x
2
+ (−6a + 11b)x − 6b + Q(x)
Since Q(x) only has quadratic, linear, and constant terms, the only quartic (4th
degree) and cubic terms are in terms of a and b. For the 4th power terms to be
the same we need
a = 1
c
2018 MathTutorDVD.com 41

For the cubic terms to both be zero, we need
0 = −6a + b = −6 + b
which means
b = 6
Therefore, the linear term that is left is
ax + b = x + 6
Plugging in these values of a, b into the whole expression, we have
x
4
= x64 + 0x
3
+ (−25x
2
) + (60x) − 36 + Q(x)
which means that
Q(x) = 25x
2
− 60x + 36
for all the terms to be equal to zero. Therefore we can write
x
4
(x − 1)(x − 2)(x − 3)
= x + 6 +
25x
2
− 60x + 36
(x − 1)(x − 2)(x − 3)
Since the quotient has degree of the numerator equal to two and degree of the
denominator equal to three, we can do a partial fractions expansion. There are
no quadratic terms or powers to make the expansion more complicated. We write
25x
2
− 60x + 36
(x − 1)(x − 2)(x − 3)
=
A
x − 1
+
B
x − 2
+
C
x − 3
Multiplying through by (x − 1)(x − 2)(x − 3) gives
25x
2
− 60x + 36 = A(x − 2)(x − 3) + B(x − 1)(x − 3) + C(x − 1)(x − 2)
which is true for all x. It is true at x = 1; there,
25 − 60 + 36 = A(1 − 2)(1 − 3) + 0B + 0C
which means
1 = 2A
c
2018 MathTutorDVD.com 42

or
A =
1
2
It is true at x = 2; there,
25(4) − 60(2) + 36 = 0A + B(2 − 1)(2 − 3) + 0 C
or
16 = −B
which means
B = −16
It is true at x = 3; there,
25(9) − 60(3) + 36 = 0A + 0B + C(3 − 1)(3 − 2)
or
81 = 2C
which means
C =
81
2
Then, the partial fractions expansion of the quotient is
1
2
x − 1
+
−16
x − 2
+
81
2
x − 3
Factoring in the linear term that is the result of long division, we get the answer:
x + 6 +
1
2
x − 1
−
16
x − 2
+
81
2
x − 3
.
c
2018 MathTutorDVD.com 43

3(i). Answer: x − 2 +
−4
x − 1
+
−3
2
(x − 1)
2
+
−2x −
1
2
x
2
+ 1
. Here, the degree of the numer-
ator is 5 and the degree of the denominator is 4, so we need to perform long
division. We write
x
5
− 4x
4
(x − 1)
2
(x
2
+ 1)
= P (x) +
Q(x)
(x − 1)
2
(x
2
+ 1)
for two polynomials P, Q where P is the quotient and Q is the remainder. We
know that P (x) is a line of the form ax + b since the difference in the degrees is
only one; a 5th degree divided by a 4th degree will be a line. Since the degree of
the denominator is 4, Q is no more than a cubic. We multiply through and write
x
5
− 4x
4
= (ax + b)(x − 1)
2
(x
2
+ 1) + Q(x)
We need to calculate the expansion. We write
(x − 1)
2
(x
2
+ 1) = (x
2
− 2x + 1)(x
2
+ 1) = x
4
− 2x
3
+ 2x
2
− 2x + 1
Then,
(ax + b)(x
4
−2x
3
+ 2x
2
−2x + 1) = ax
5
+ (−2a + b)x
4
+ (2a −b)x
3
+ (−2a + b)x + b
Since Q(x) is no more than a cubic, the terms of x
5
and x
4
must be equal just
based on this expression. We write
x
5
− 4x
4
= ax
5
+ (−2a + b)x
4
For the first coefficients to be equal,
a = 1
For the second coefficients to be equal,
−2a + b = −4
which means
b = −2
c
2018 MathTutorDVD.com 44

Then, we expand
x
5
− 4x
4
= (x − 2)(x − 1)
2
(x
2
+ 1) + Q(x)
as
x
5
− 4x
4
= x
5
− 4x
4
+ 6x
3
− 6x
2
+ 5x − 2 + Q(x)
This means that
Q(x) = −6x
3
+ 6x
2
− 5x + 2
In other words, the result of our polynomial division is that
x
5
− 4x
4
(x − 1)
2
(x
2
+ 1)
= x − 2 +
−6x
3
+ 6x
2
− 5x + 2
(x − 1)
2
(x
2
+ 1)
This last term is the ratio of a cubic to a quartic. Since the degree of the numerator
is lower than the denominator, we can write it as a partial fractions expansion.
The partial fractions decomposition technique tells us that
−6x
3
+ 6x
2
− 5x + 2
(x − 1)
2
(x
2
+ 1)
=
A
x − 1
+
B
(x − 1)
2
+
Cx + D
x
2
+ 1
where the irreducible quadratic term is because x
2
+1 has no real roots and does
not factorize. To solve for A, B, C, D we can multiply through by (x − 1)
2
(x
2
+ 1)
to get
−6x
3
+ 6x
2
− 5x + 2 = A(x − 1)(x
2
+ 1) + B(x
2
+ 1) + (Cx + D) (x − 1)
2
This is true for all values of x; it is true at x = 1 where
−6 + 6 − 5 + 2 = 0A + 2B + 0
which means that
B =
−3
2
At x = 0, we have
2 = A(−1)(1) +
−3
2
(1) + (0C + D)(−1)
2
c
2018 MathTutorDVD.com 45

which means
7
2
= −A + D
For the x
3
terms to be equal, we need
−6 = A + C
Finally, we can evaluate at x = 2 to get
−6(8) + 6(4) − 5(2) + 2 = A(1)(5) +
−3
2
(5) + (2C + D)
which means
−32 = 5A −
15
2
+ 2C + D
Substituting
7
2
= −A + D we have
−32 = 6A −
15
2
+ 2C +
7
2
or
6A + 2C = −28
Combined with
−6 = A + C
we see that
4A = −16
or
A = −4
which means that
D =
7
2
+ A = −
1
2
and
C = −6 − A = −2
Then, the answer (finally!) of the form
A
x−1
+
B
(x−1)
2
+
Cx+D
x
2
+1
is
−4
x − 1
+
−3
2
(x − 1)
2
+
−2x −
1
2
x
2
+ 1
c
2018 MathTutorDVD.com 46

Including the linear term
P (x) = x − 2
we get the answer: x − 2 +
−4
x − 1
+
−3
2
(x − 1)
2
+
−2x −
1
2
x
2
+ 1
.
c
2018 MathTutorDVD.com 47

4. Solve the following indefinite integrals using the partial fractions decomposition tech-
nique:
4(a). Answer. ln |x| − ln |x + 1| + C . None of the Calculus I techniques help us to
solve this problem, so we need to use partial fractions. We want to write the
integrand
1
x(x + 1)
=
A
x
+
B
x + 1
for some A, B. This is a useful technique here because
A
x
and
B
x+1
are easily
integrable. We already calculated the partial fraction decomposition by solving
for A, B earlier in this worksheet. Briefly, we did it by multiplying through to write
1 = A(x + 1) + Bx
At x = 0 we see that
A = 1
and at x = −1 we see that
B = −1
Therefore
1
x(x + 1)
=
1
x
−
1
x + 1
Both of these functions are integrable with techniques from Calculus I. We write
Z
1
x(x + 1)
dx =
Z
1
x
−
1
x + 1
dx =
Z
1
x
dx −
Z
1
x + 1
dx
The first integral is
Z
1
x
dx = ln |x| + C
To solve the second integral we make the u substitution
u = x + 1
Then
du
dx
= 1
c
2018 MathTutorDVD.com 48

and
du = dx
so the integral is
Z
1
x + 1
dx =
Z
1
u
du = ln |u| + C = ln |x + 1| + C
Then, since the two constants of integration combine into one, our answer is
ln |x| − ln |x + 1| + C .
c
2018 MathTutorDVD.com 49

4(b). Answer: 28 ln
x +
1
3
− 27 ln
x +
1
4
. Again, none of familiar Calculus I tech-
niques work here. Instead we need to use partial fractions to rewrite the inte-
grand:
x − 2
x +
1
3
x +
1
4
=
A
x +
1
3
+
B
x +
1
4
for some A, B. We solve for A, B by multiplying through by
x +
1
3
x +
1
4
to get
x − 2 = A
x +
1
4
+ B
x +
1
3
At x = −
1
4
, the first term cancels, leaving us with
−
9
4
= B
−
1
4
+
1
3
or
B = −27
At x = −
1
3
, the second term cancels, leaving us with
−
7
3
= A
−
1
3
+
1
4
or
A = 28
So the decomposition is
x − 2
x +
1
3
x +
1
4
=
28
x +
1
3
−
27
x +
1
4
Both of these terms are integrable by Calculus I techniques. We evaluate
Z
28
x +
1
3
−
27
x +
1
4
dx =
Z
28
x +
1
3
dx −
Z
27
x +
1
4
dx
Both of these integrals can be solved using u-substitutions; the first by the u-
substitution of u = x +
1
3
and the second by the u-substitution of u = x +
1
4
. The
first integral is
Z
28
x +
1
3
dx = 28 ln
x +
1
3
+ C
c
2018 MathTutorDVD.com 50

and the second integral is
Z
27
x +
1
4
dx = 27 ln
x +
1
4
+ C
so the answer is 28 ln
x +
1
3
− 27 ln
x +
1
4
.
c
2018 MathTutorDVD.com 51

4(c). Answer: −
1
12
ln |x + 1| +
4
3
ln |x − 2| −
9
4
ln |x − 3| + C . Once again, none of
the familiar Calculus I techniques work to solve this problem. There is no u-
substitution we can make. However, partial fractions decomposition helps break
the integrand down into pieces that are more easily integrable. We write
−x
2
(x + 1)(x − 2)(x − 3)
=
A
x + 1
+
B
x − 2
+
C
x − 3
for some A, B, C. To find A, B, C we multiply through by (x + 1)(x − 2)(x − 3) to
see that
−x
2
= A(x − 2)(x − 3) + B(x + 1)(x − 3) + C(x + 1)(x − 2)
for all x and some A, B, C. At x = −1 this means that
−1 = A(−1 − 2)(−1 − 3) + 0B + 0C
or
A =
−1
12
At x = 2 this means that
−4 = 0A + B(2 + 1)(2 − 3) + 0C
or
B =
4
3
At x = 3 this means that
−9 = 0A + 0B + C(3 + 1)(3 − 2)
or
C =
−9
4
This means that the decomposition is
Z
−
x
2
(x + 1)(x − 2)(x − 3)
dx =
Z
−1
12
x + 1
+
4
3
x − 2
+
−9
4
x − 3
dx
c
2018 MathTutorDVD.com 52

Each of these parts is easily integrable; we just need to integrate them in turn:
−
1
12
Z
1
x + 1
dx +
4
3
Z
1
x − 2
dx −
9
4
Z
1
x − 3
dx
so the answer is −
1
12
ln |x + 1| +
4
3
ln |x − 2| −
9
4
ln |x − 3| + C .
c
2018 MathTutorDVD.com 53

4(d). Answer: ln |x + 1| +
2
x + 1
−
3
(x + 1)
2
+ C . Again we seek to expand by partial
fractions. The form of the partial fractions expansion of
x
2
+5
(x+1)
3
is
A
x + 1
+
B
(x + 1)
2
+
C
(x + 1)
3
for some A, B, C. To solve for A, B, C we solve:
x
2
+ 5
(x + 1)
3
=
A
x + 1
+
B
(x + 1)
2
+
C
(x + 1)
3
Multiplying through by (x + 1)
3
gives us
x
2
+ 5 = A(x + 1)
2
+ B(x + 1) + C
At x = −1 we have
1 + 5 = 0A + 0B + C
or
C = 6
We also see that the coefficients of x
2
on both sides have to be equal. On the left
side this coefficient is 1 and on the right side it is A so
A = 1
Finally, at 0,
5 = A + B + C = 1 + B + 6
so
B = −2
Then, we have that
Z
x
2
+ 5
(x + 1)
3
dx =
Z
1
x + 1
−
2
(x + 1)
2
+
6
(x + 1)
3
dx
=
Z
1
x + 1
dx − 2
Z
1
(x + 1)
2
dx + 6
Z
1
(x + 1)
3
dx
c
2018 MathTutorDVD.com 54

Each of these terms can be integrated using techniques from Calculus I. The first
term is
Z
1
x + 1
dx = ln |x + 1| + C
The second term is
Z
1
(x + 1)
2
dx
This can be solved by a u-substitution of
u = x + 1
and
du = dx
Then,
Z
1
(x + 1)
2
dx =
Z
1
u
2
du = −
1
u
+ C = −
1
x + 1
+ C
The third term is
Z
1
(x + 1)
3
dx = −
1
2
1
(x + 1)
2
+ C
Then, we compute the sum of the terms:
ln |x + 1| − 2
−
1
x + 1
+ 6
−
1
2
1
(x + 1)
2
+ C
evaluates to ln |x + 1| +
2
x + 1
−
3
(x + 1)
2
+ C .
c
2018 MathTutorDVD.com 55

4(e). Answer: ln |x| −
1
2
ln
x
2
+ 1
+ C . We expand by partial fractions. We note
that x
2
+ 1 is an irreducible quadratic that has no real roots. According to the
partial fractions decomposition technique, we can write
1
x(x
2
+ 1)
=
A
x
+
Bx + C
x
2
+ 1
for some A, B, C. Multiplying through by x(x
2
+ 1) we see that
1 = A(x
2
+ 1) + (Bx + C)(x)
At x = 0 we have
1 = A(1) + (0B + C)(0)
so
A = 1
Then,
1 = x
2
+ 1 + Bx
2
+ Cx
for all x. For this to be true (for all the coefficients to match),
B = −1
and
C = 0
Then,
1
x(x
2
+ 1)
=
1
x
−
x
x
2
+ 1
We write
Z
1
x
−
x
x
2
+ 1
dx =
Z
1
x
dx −
Z
x
x
2
+ 1
dx
The first integral is just
Z
1
x
dx = ln |x| + C
The second integral requires a u-substitution of
u = x
2
+ 1
c
2018 MathTutorDVD.com 56

Then,
du
dx
= 2x
and
dx =
1
2x
du
So we can write
Z
x
x
2
+ 1
dx =
Z
x
u
·
1
2x
du =
1
2
Z
1
u
du
This is just
1
2
ln |u| + C =
1
2
ln
x
2
+ 1
+ C
where we do not need the absolute value because x
2
+ 1 is always positive.
Therefore the answer is ln |x| −
1
2
ln
x
2
+ 1
+ C .
c
2018 MathTutorDVD.com 57

5. Challenge. Solve the following indefinite integrals using the partial fractions decom-
position technique:
5(a). Answer:
x
2
2
+ x +
1
3
ln |x − 1| −
2
3
ln
x
2
+ 2
−
2
√
2
3
tan
−1
x
√
2
+ C . We cannot
proceed directly to partial fractions because the degree of the numerator is higher
than the degree of the denominator. We need to divide the polynomial so that the
degree of the numerator becomes less than the degree of the denominator. To
divide
x
4
x
3
− x
2
+ 2x − 2
we see that the linear term is x; that is, the denominator goes x times into the
numerator because then the 4th power term of the numerator cancels. We write
x
4
x
3
− x
2
+ 2x − 2
=
x(x
3
− x
2
+ 2x − 2) + x
3
− 2x
2
+ 2x
x
3
− x
2
+ 2x − 2
= x +
x
3
− 2x
2
+ 2x
x
3
− x
2
+ 2x − 2
Then the denominator goes once more into the numerator so this is equal to
x + 1 +
−x
2
+ 2
x
3
− x
2
+ 2x − 2
Having performed the long division, we need to integrate
Z
x + 1 +
−x
2
+ 2
(x − 1)(x
2
+ 2)
dx
This last term requires a partial fractions expansion. We write
−x
2
+ 2
(x − 1)(x
2
+ 2)
=
A
x − 1
+
Bx + C
x
2
+ 2
for some A, B. Multiplying through by (x − 1)(x
2
+ 2) we get
−x
2
+ 2 = A(x
2
+ 2) + (Bx + C)(x − 1)
for all x and some A, B, C. At x = 1 we have
−1 + 2 = A(1 + 2) + (B + C)(0)
which means
A =
1
3
c
2018 MathTutorDVD.com 58

For the x
2
terms to be equal we have
−1 = A + B
so
B =
−4
3
For the constant terms to be equal we have
2 = 2A − C
so
C = 2A − 2 = −
4
3
Then the partial fractions expansion is
−x
2
+ 2
(x − 1)(x
2
+ 2)
=
1
3
x − 1
−
4
3
x + 1
x
2
+ 2
and we need to integrate
Z
x + 1 +
1
3
x − 1
−
4
3
x + 1
x
2
+ 2
dx =
Z
(x + 1) dx +
1
3
Z
1
x − 1
dx −
4
3
Z
x + 1
x
2
+ 2
dx
The first integral is
Z
(x + 1)dx =
x
2
2
+ x + C
The second integral is
1
3
Z
1
x − 1
dx =
1
3
ln |x − 1| + C
The third integral is tricker. We actually need to break it up again to write
Z
x + 1
x
2
+ 2
dx =
Z
x
x
2
+ 2
dx +
Z
1
x
2
+ 2
dx
We compute the first integral by substituting
u = x
2
+ 2
so
du =
1
2x
dx
c
2018 MathTutorDVD.com 59

and then
Z
x
x
2
+ 2
dx =
1
2
Z
1
u
du =
1
2
ln |u|du =
1
2
ln
x
2
+ 2
+ C
which is then multiplied by the coefficient
−4
3
to yield
−2
3
ln
x
2
+ 2
+ C
The second integral is similar to the derivative of arctangent, which is
1
x
2
+1
. So
we substitute
u =
x
√
2
and then
du
dx
=
1
√
2
so
dx =
√
2du
Then,
Z
1
x
2
+ 2
dx =
√
2
Z
1
√
2u
2
+ 2
du =
√
2
Z
1
2u
2
+ 2
du =
√
2
2
Z
1
u
2
+ 1
du
which is
√
2
2
tan
−1
u + C
so the solution for this final piece is
−
4
3
·
√
2
2
tan
−1
x
√
2
+ C
Then adding all the pieces together we get the answer
x
2
2
+ x +
1
3
ln |x − 1| −
2
3
ln
x
2
+ 2
−
2
√
2
3
tan
−1
x
√
2
+ C .
c
2018 MathTutorDVD.com 60

5(b). Answer: ln |x| −
1
2
ln
x
2
+ 2x + 4
−
√
3
3
tan
−1
x + 1
√
3
+ C . We seek to decom-
pose the integrand into partial fractions. By the partial fractions decomposition
technique, the answer will be of the form
A
x
+
Bx + C
(x
2
+ 2x + 4)
since x
2
+ 2x + 4 is an irreducible quadratic. We solve
4
x(x
2
+ 2x + 4)
=
A
x
+
Bx + C
x
2
+ 2x + 4
for some A, B, C. Multiplying through, we have that
4 = A(x
2
+ 2x + 4) + (Bx + C)x
At x = 0 we have
4 = 4A
so
A = 1
For the quadratic term to be equal we need
0 = Ax
2
+ Bx
2
so
A + B = 0
so
B = −1
For the linear term to be equal we need
2A + C = 0
so
C = −2
c
2018 MathTutorDVD.com 61

Then the partial fractions expansion is
4
x(x
2
+ 2x + 4)
=
1
x
+
−x − 2
x
2
+ 2x + 4
The integral of the first part is
Z
1
x
= ln |x| + C
The other part is a little tricker. We simplify
−
Z
x + 2
x
2
+ 2x + 4
dx = −
Z
x + 1
x
2
+ 2x + 4
+
1
x
2
+ 2x + 4
dx
We need to split up the two terms so that we can use the convenient u-substitution,
u = x
2
+ 2x + 4 and
du
dx
= 2x + 2
to reduce it. We solve
−
Z
x + 1
x
2
+ 2x + 4
dx = −
Z
x + 1
u
1
2x + 2
du = −
1
2
Z
1
u
du
so this integral evaluates to
−
1
2
ln
x
2
+ 2x + 4
Finally, we can solve
−
Z
1
x
2
+ 2x + 4
with a convenient trigonometric substitution. If we let
u = x + 1
then
du = dx
and this is
−
Z
1
(x + 1)
2
+ 3
dx = −
Z
1
u
2
+ 3
du
c
2018 MathTutorDVD.com 62

Then we need another u-substitution (to avoid confusion about the variables, we
can call it a w-substitution) of
w =
u
√
3
and
dw
du
=
1
√
3
so
du =
√
3dw
Then we write
−
Z
1
u
2
+ 3
du = −
√
3
3
Z
1
w
2
+ 1
dw = −
√
3
3
tan
−1
w + C
Substituting for w in terms of u and then u in terms of x we evaluate this integral
as
−
√
3
3
tan
−1
x + 1
√
3
+ C
Putting together the pieces the answer is ln |x| −
1
2
ln
x
2
+ 2x + 4
−
√
3
3
tan
−1
x + 1
√
3
+ C .
c
2018 MathTutorDVD.com 63

5(c). Answer: ln |sin x| − ln |sin x + cos x| + C . This can also be solved by partial
fractions even though there are sines and cosines instead of polynomial terms.
Since
sin
2
x + sin x cos x = sin x (sin x + cos x)
we want to see if
1
sin
2
x + sin x cos x
=
A
sin x
+
B
sin x + cos x
for some constants A, B. Multiplying through, we get
1 = A (sin x + cos x) + B sin x
What if the right side could be manipulated to be in the form sin
2
x + cos
2
x which
would indeed equal to 1? For this to happen, we try to rewrite it as
(A + B) sin x + A cos x
For this to be equal to sin
2
x + cos
2
x, we would need
A = cos x
and
A + B = sin x
which means
B = sin x − cos x
Then,
A (sin x + cos x) + B sin x = 1
So we have an equivalent integral:
Z
1
sin
2
x + sin x cos x
dx =
Z
cos x
sin x
+
sin x − cos x
sin x + cos x
dx
At first glance, this seems to overcomplicate things. But actually both of these
forms happen to be easily integrable. To solve
Z
cos x
sin x
dx
c
2018 MathTutorDVD.com 64

we make the u-substitution of
u = sin x
Then,
du
dx
= cos x
and
dx =
1
cos x
du
Then,
Z
cos x
sin x
dx =
Z
cos x
u
1
cos x
du =
Z
1
u
du = ln |u| + C
so the first integral is
ln |sin x| + C
To solve
Z
sin x − cos x
sin x + cos x
dx
we make another u-substitution of
u = sin x + cos x
Then,
du
dx
= cos x − sin x
and
dx =
1
cos x − sin x
du
so the integral reduces to
Z
sin x − cos x
u
·
1
cos x − sin x
du = −
Z
du
u
= −ln |u|
which is
−ln |sin x + cos x| + C
All of the simplifications work out just right to yield the neat answer of
ln |sin x| − ln |sin x + cos x| + C .
c
2018 MathTutorDVD.com 65
